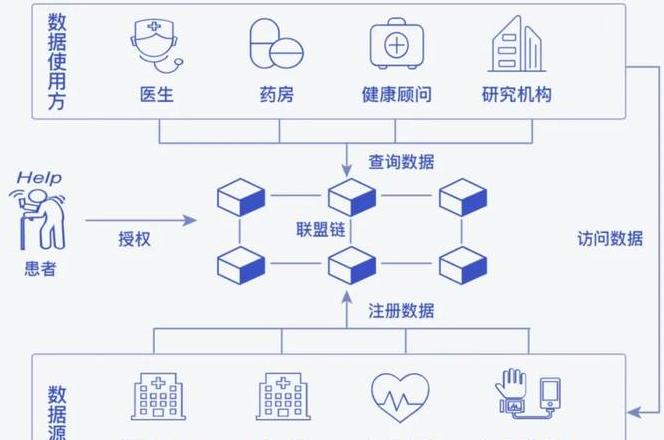
˙▽˙ Bitcoins Höhe verschärft den Mangel an Chip. Wie ist die Beziehung zwischen Bitcoin und Chips?
Die Zunahme von Bitcoin verschärft den Mangel an Chip. Bitcoin ist eigentlich eine Reihe digitaler Schlüssel. Bitcoin "Mining" ist, Antworten auf diese digitalen Schlüssel zu finden. Bitcoin benötigt "Bergbau" viel Computing. Um die Berechnung von Flüssigkeiten aufrechtzuerhalten, müssen Computer relativ erweiterte Konfigurationen aufweisen. Computer werden durch Chips gesteuert. Bitcoin -Transaktionen oder "Mining" erfordern Computer, um Computer zu übergeben, sodass sie relevant sind.
Bitcoin als aufstrebende Branche hat uns immer Überraschungen gebracht. Der Preis hat sich vor mehr als zehn Jahren um Zehntausende von Male erhöht, sodass jeder die Magie von Bitcoin spüren konnte. Bitcoin ist im Internet. Bitcoin -Transaktionen und -Anquisitionen erfordern Computer, und es gibt keine Bedeutung für Bitcoin ohne Computer. Da immer mehr Menschen an Bitcoin oder Bitcoin teilnehmen, wird dies definitiv zu einer hohen Nachfrage nach Computerausrüstung führen. Chips sind der wichtigste Teil von Computern. Die Zunahme der Computergeräte wird definitiv zu einer Zunahme der Chips führen, was zu einem Mangel an Chips führt.
1. Bitcoin -Transaktionen oder "Mining" können nicht von Computern getrennt werden.
Ich denke, jeder ist sich der Komponenten von Computern bewusst. Chips sind die wichtigsten Komponenten von Computern. Ohne Chips können Computer überhaupt nicht arbeiten. Bitcoin hängt von Online -Transaktionen und -entwicklung ab. Die Beziehung zwischen Bitcoin und Kartoffeln ist in der Tat die Beziehung zwischen Fisch und Wasser, und niemand kann auf irgendjemanden verzichten. Dies ist die Beziehung zwischen Chips und Bitcoin.
2. Bitcoin "Mining" verbraucht viel Computer, was zu einer kontinuierlichen Zunahme der Computergeräte führt.
Wir alle wissen, dass es nur zwei Möglichkeiten gibt, Bitcoin zu bekommen. Einer von ihnen ist die Auflage, den Kauf und den Verkauf von Bitcoin direkt, und der andere ist "Minen", um Bitcoin zu finden. Beide Methoden erfordern eine große Anzahl von Computergeräten, und die Anforderungen an Computergeräte sind relativ hoch. Angesichts der Zunahme der Anzahl der Personen, die "meinen" und mehr Anforderungen an Computerausrüstung "" meinen "Mine", wird dies definitiv zu einem Mangel an Chips führen, der die Bereitstellung von Chips beeinflusst.
Bitcoin als aufstrebende Branche hat uns eine neue Hoffnung auf Wohlstand gegeben, aber der Verlust elektronischer Produkte und der elektronische Energieverbrauch durch Bitcoin sind auch Probleme, mit denen wir konfrontiert sind.
≥△≤ Wie Schül
er die Bitcoin -Kryptographie -Algorithmen verstehen. Das öffentliche Schlüsselsystem von Bitcoin verwendet einen elliptischen Kurvenalgorithmus, um die Sicherheit der Transaktion zu gewährleisten. Dies liegt daran, dass einzelne logarithmische Probleme konfrontiert werden müssen, um die elliptische Kurvenverschlüsselung zu überwinden. Bisher wurden in der Polynomzeit keine Lösungen gefunden. Es wird als sicher angesehen, wenn der im Algorithmus verwendete Raum groß genug ist. Dieser Artikel enthält keine fortgeschrittene mathematische Theorie und hofft, dass alle Schüler sie verstehen werden.Kryptographie hat eine lange Geschichte, und fast jeder kann Verschlüsselungs- und Entschlüsselungsmethoden erstellen. Alte oder einfache Methoden erfordern einen vertraulichen Verschlüsselungsalgorithmus und einen privaten Schlüssel. Aufgrund der langfristigen offensiven und defensiven Kämpfe im Laufe der Geschichte ist die Vertraulichkeit auf Verschlüsselung jedoch unzuverlässig. Gleichzeitig ist das Senden von Geheimtasten seit langem ein großes Problem, und sie stehen häufig vor dem Risiko, geheimen Schlüssellecks und Mittelwegangriffen zu begegnen.
In den 1970er Jahren führte die Verschlüsselung zu einem Durchbruch. Ralph C. Merkle schlug 1974 erstmals die Idee der asymmetrischen Verschlüsselung vor. Zwei Jahre später schlugen zwei Gelehrte Whitfielddiffie und Whitfielddiffie spezifische Ideen vor, die auf Einweg-Merkmalen und Einweg-Geheimtormerkmalen basieren. Seitdem sind eine Reihe von Studien und Algorithmen entstanden, von denen das bekannteste der RSA -Algorithmus und eine Reihe von elliptischen Kurvenalgorithmen sind.
Egal welcher Algorithmus auf den Schultern seiner Vorgänger steht, er basiert hauptsächlich auf der Entwicklung von Zahlen, Gruppentheorie und Finite -Domänen -Theorie. Der geheime Schlüssel zum Verschlingen von Inhalten muss nicht übergeben werden und wird von der Operation generiert, wodurch die Kommunikation auch in unsicheren Netzwerken sichern wird. Kryptografische Risse hängen vom Riss des geheimen Schlüssels ab, aber das Riss des geheimen Schlüssels hat Schwierigkeiten. Für den RSA -Algorithmus ist dieses Problem eine große Anzahl von Faktorisierungen, und für den elliptischen Kurvenalgorithmus ist dieses Problem eine diskrete logarithmische Lösung. Derzeit gibt es keine Lösung für die Polynomzeit. Mit anderen Worten, der Schwierigkeitsgrad steigt exponentiell an, wenn die Anzahl die Anzahl erhöht.
Wie wird Verschlüsselung und Entschlüsselung auf öffentlichen und privaten Schlüsselsystemen durchgeführt? Kurz gesagt, sowohl Verschlüsselung als auch Entschlüsselung müssen genau sein und daher durch Operationen innerhalb einer endlichen Domäne durchgeführt werden. Ein endliches Feld ist eine Sammlung endlicher Elemente. Die Verschlüsselung bildet ein Element einem anderen, und die Entschlüsselung wird erneut abgebildet. Die Finite -Domänen -Konfiguration bezieht sich auf die Eigenschaften von Primzahlen.
Vor einiger Zeit, als Riemanns Vermutung (das eng mit dem Prime -Theorem verwandt ist) stark übertrieben war, sagte der technische Direktor des Blockchain -Projekts, dass der Algorithmus für elliptische Kurven nichts mit Primzahlen zu tun hat und nicht durch den Beweis von Riemanns Eintritt beeinflusst wird. Es gibt eine Vielzahl von Blockchain -Projekten und Sie können sehen, dass Sie sie wirklich sorgfältig waschen müssen.
Das in Bitcoin und die meisten Blockchain -Projekte verwendete öffentliche Schlüsselsystem ist eher ein elliptischer Kurvenalgorithmus als RSA. Vor der Einführung eines elliptischen Kurvenalgorithmus ist es sehr hilfreich, diskrete logarithmische Probleme für seine Sicherheit zu verstehen.
Schauen wir uns zuerst den Theorem von Fermat an. Die Ganzzahl A mit der Reihenfolge von Modulo P ist (max) p-1.
Zwei Theoreme:
Basierend darauf können wir sehen, dass {1,2,3, p-1} eine endliche Domäne ist und dass die Definitionsoperation GI (MODP) in diese endliche Domäne passt. Gleichzeitig ist das Betriebsergebnis unterschiedlich, wenn Sie eine andere Zahl von 0 bis P-2 einnehmen. Dies ist im Grunde dasselbe, was wir in der High School gelernt haben, außer dass es eine zusätzliche Schicht elastischer Berechnungen gibt.
Ein weiterer Punkt in einem anderen Punkt ist, dass der Exponent von G möglicherweise nicht auf 0-P-2 begrenzt ist, aber in Wirklichkeit kann es alle natürlichen Zahlen sein, während
daran liegt, dass alle Funktionswerte endliche Domänen sind und kontinuierliche Schleifen sind.
diskrete logarithmische Definition: Sei G das ursprüngliche Wurzel von Modulo p, und (a, p) = 1,
Aufgerufen werden (für das ursprüngliche Stamm von Modulo P), ausgedrückt wie folgt, wobei die ersten drei Zeichen des Index diese Definition sehr ähnlich der Definition in einem Protokoll in einem Protokoll sind? Tatsächlich ist dies eine Erweiterung der logarithmischen Definitionen, die ich in der High School gelernt habe, aber jetzt wird sie auf die endliche Domäne angewendet.
Dies unterscheidet sich jedoch von logarithmischen Berechnungen der tatsächlichen Domänen. Die tatsächliche Domäne ist ein kontinuierlicher Raum. Logarithmische Berechnungen dazu haben Formeln und Regeln zu befolgen, aber die Genauigkeit ist oft schwer zu erreichen. Kryptografische Systeme erfordern Präzision, aber es ist äußerst schwierig, in endlichen Bereichen zu arbeiten. Wenn Sie den Leistungswert A und die logarithmische Basis G kennen, ist es sehr schwierig, diesen diskreten logarithmischen Wert i zu finden.
Wenn die ausgewählte Primzahl P groß genug ist, ist es unmöglich, mich in Bezug auf den berechneten Betrag zu finden. Ich kann also sagen, dass ich es nicht berechnen kann. Das heißt, es ist sicher und nicht geknackt.
elliptischer Kurvenalgorithmus von Bitcoin verwendet speziell den SecP256K1 -Algorithmus. Es gibt viele Einführungen in elliptische Kurvenalgorithmen im Internet. Ich werde hier nicht ins Detail gehen. Soweit Sie wissen, ist es eigentlich keine elliptische Funktion) und die Definition lautet:
und es gibt Parameter a und b. Unterschiedliche Werte verursachen unterschiedliche elliptische Kurven. Natürlich sind X und Y hier in realen Bereichen definiert, aber dies ist in einem kryptografischen System nicht möglich. Wenn tatsächlich angenommen wird, müssen X und Y in einer endlichen Domäne definiert werden. Da die endliche Domäne eine natürliche Zahl ist und kleiner als Prime P ist, spiegelt diese elliptische Kurve definiert, und spiegelt die individuellen Punkte im Koordinatensystem wider. Dies ist nicht wie eine Kurve. In den endlichen Feldern des Sets werden die verschiedenen Operationen jedoch abgeschlossen. Das heißt, die entspre chenden Punkte können durch den Verschlüsselungsvorgang gefunden werden, und die vorgekrönten Punkte können durch den Entschlüsselungsvorgang erhalten werden.
Gleichzeitig möchten wir eine endliche Untergruppe im diskreten Gitter dieser elliptischen Kurve mit den oben genannten Traversal- und periodischen Eigenschaften wie im oh2en diskreten logarithmischen Problem finden. Und alle Berechnungen verwenden diese Untergruppe. Dies schafft die erforderlichen endlichen Domänen. Als nächstes benötigen wir die Reihenfolge der Untergruppen (Prime N) und den Basispunkt G der Untergruppen (Koordinaten, die durch die Subgruppen der N-Ordnung durch die Add-Operation durchquert werden können).
Gemäß der oh2en Erklärung können wir sehen, dass die Definition einer elliptischen Kurve fünfgliedrige Vorfahren umfasst (p, a, b, g, n, h). The specific definitions and concepts are:
p: The large prime A, B: the elliptic curve function parameters used to define the finite domain (group) of p: the elliptic curve A, the base point of the cyclic subgroup, and the basis of operation n:n:cycloups n:cycloups n:cycloups n:subgroups, i.e. the order of the groups is divided by the ganzzahliger Teil der Reihenfolge der Untergruppen.
Jetzt ist es Zeit zu sehen, ob es sich um den elliptischen Kurvenalgorithmus von Bitcoin handelt. Einfach ausgedrückt, es ist eine elliptische Kurve mit den oh2en Werten.
Die elliptische Kurve ist definiert als zwei miteinander verbundene Punkte, und der symmetrische Punkt des dritten Punktes im Bild in Bezug auf die x-Achse ist die Summe der beiden Punkte. In diesem Teil des Internets gibt es bereits viele Inhalte, und Details werden hier nicht erläutert.
sorgfältige Schüler können jedoch Fragen haben. Das Problem mit dem diskreten logarithmischen Problem ist, dass es leicht ist, einen Exponenten zu finden, aber es ist sehr schwierig, diesen Exponenten zu finden. Im elliptischen Kurvenalgorithmus gibt es jedoch keinen Exponenten, nur das Produkt. Wie spiegelt dies das diskrete logarithmische Problem wider?
In der Tat ist dies eine Frage der Definition. Wenn der elliptische Kurvenalgorithmus ursprünglich definiert wurde, wurde diese Art von Operation als Summe definiert. Solange Sie diese Art von Operation als Produkt definieren, gibt es kein Problem mit dem gesamten System. Es zeigt auch, dass alle Vorgänge, wenn sie als Produkt definiert sind, mit den diskreten logarithmischen Problemen des Formulars übereinstimmen und mit dem Prinzip der endlichen Domänenauswahl übereinstimmen. Dies ist also im Wesentlichen immer noch ein separates logarithmisches Problem. Aber es ist kein völlig einfaches separates logarithmisches Problem. In Wirklichkeit ist es schwieriger als ein typisches diskretes logarithmisches Problem. Denn hier finden wir nicht nur den diskreten Logarithmus der Zahlen, sondern auch die gleichen Werte wie der diskrete Logarithmus einer benutzerdefinierten Berechnung. Dies ist auch der Grund, warum es sehr sicher ist, weitaus weniger private Schlüsselbits (256 Bit) zu verwenden, als RSA erforderlich ist (normalerweise 2048 Bit).
≥△≤ Wie man den geheimen Schlüssel im Transaktionsprozess liest
Suchen Sie nach der Spalte zur Produktkennung, die der Schlüssel zum Produkt ist. Um die geheime Taste in der Transaktionskette anzuzeigen, müssen Sie im Allgemeinen auf die rechte Maustaste klicken, um das Computermenü zu öffnen, die Merkmalsspalte zu finden, zu öffnen und dann nach der Produktkennungspalte in der Sprungfunktionsplatte zu suchen, die die Schlüssel des Produkts ist. Es ist zu beachten, dass eine Kopie des Schlüssels eine Bitcoin -Kontokontrolle hat. Bitcoin -Transaktionen erfordern eine gültige Signatur in Blockchain. Salehs Schlüssel kann nur eine gültige digitale Signatur erstellen. Eine Kopie des Schlüssels hat daher eine Bitcoin -Kontokontrolle. Kann ich ̄□ ̄|| Bitcoin knacken?
Bitcoin ist fast unmöglich zu knacken.
Die Gründe sind wie folgt: Bitcoin-Liste: Bitcoin-Bitcoin-Konten, die mit dem vertraulichen Schlüssel-Room-Konto der geheimen Schlüssel-Bo-Address eingerichtet sind. Bitcoin Cracks beginnt tatsächlich, die Schachtel oder die Schachtel zu knacken, um die wirklich sehr schwierige Taste zu knacken. Einschränkungen des Angriffs, aber diese Methode erfordert die Einrichtung des persönlichen Lebens von Bitcoin -Inhabern, was schwierig ist, die Realität der Bitcoin -Inhaber und -Angriffe zu erreichen. Wenn Bitcoin -Inhaber diese Methode nicht beheben, es sei denn, Sie haben Gehirnkonten installiert. The difficulty of brute force cracking: The further attack is a brute force cracking, and is trying to crack a list of numbers and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and symbols and Symbole und Symbole und Symbole und Symbole und Symbole und Symbole sowie Symbole und Symbole und Symbole und Symbole sowie Symbole und Symbole und Symbole und Symbole und Symbole und Symbole und Symbole und Symbole und Symbole. Der geheime Schlüssel von Bitcoin ist jedoch in der 256-Bit-Binärzahl enthalten, die aus 256-Bit-Binärzahlen besteht. Es tritt in Dezimalzahlen ohne Dezimalzahl ein. Derzeit ist es unmöglich, den Markt für den Markt auf dem Markt zu füllen, sodass es lange dauern kann, bis er abgeschlossen ist. Einige Guangda -Computer können dieses Ziel nur haben. Diese Technologie befindet sich jedoch noch in Entwicklungsebene und wird nicht weit verbreitet.
Bitcoin von HündinDer Unterschied zwischen der Realität ist eine Diskrepanz in der Realität und es gibt nur Theorien.